Mistfahren mal ziemlich wissenschaftlich

Ausgerechnet die Anhänger des Sinclair ZX81 - eines der auf den ersten Blick unscheinbarsten Computer - sind heute, vierzig Jahre nach seiner Markteinführung, die aktivsten und verblüffen immer wieder mit neuen Hard- und Softwareprojekten.
So hat sich Ulrich vom ZX-Team eine vom “Zeddy“ angesteuerte kleine Maschine gebaut, die Ostereier bemalen kann, zu der Joachim die Programmierung beisteuerte. Sie stellten sie 2017 auf ihrem Team-Treffen und danach im Forum vor.

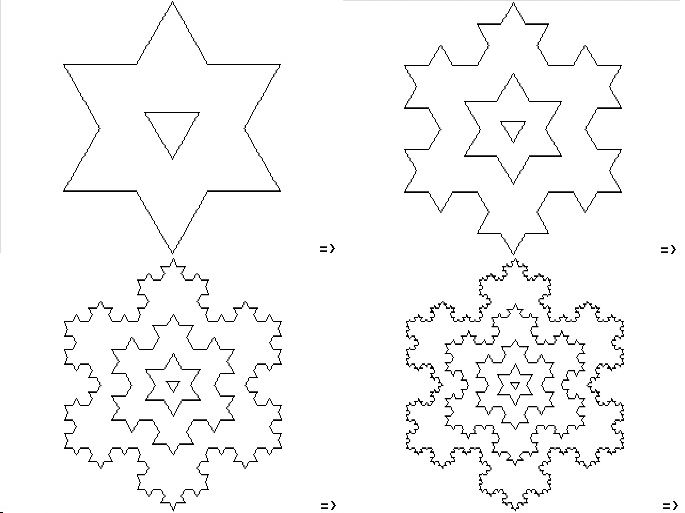
Sechs Wochen vor dem diesjährigen Osterfest stellte Joachim ein neues Muster zum Verzieren der Eier vor (siehe nebenstehenden screenshot eines YouTube-Videos) für das Wikipedia eine mehrere computerbildschirme füllende Erklärung gibt: Wikipedia Hilbert-Kurve. Es ist eine Kurve, die ein Quadrat vollständig ausfüllen kann.
Erstaunlich, was für Gedanken sich Mathematiker machen und zu welchen Resultaten sie kommen. Eine Linie bzw. Strecke hat, so lernten wir, nur eine Länge, ihre Breite ist Null. Wie zum Geier kann sie dann eine Fläche füllen? Die Antwort ist: in der Unendlichkeit, aber das können wir natürlich nicht nachprüfen. Paradox ist, dass ein endlich langes Programm genügt, das Problem anzugehen, doch ein Resultat wiederum nie wirklich geliefert werden kann.
Wie ich das meine? Das Programm enthält eine rekursive Subroutine. Rekursiv bedeutet, dass sich diese Subroutine immer wieder selbst aufruft, bis eine Abbruchbedingung erreicht ist. Diese Abbruchbedingung ist die Feinheit der Auflösung und diese Zahl bestimmt, wie oft sich die Subroutine aufruft. Hierfür benötigt das Rechenprogramm einen Stapel für die Rückkehradressen, also physisch einen Bereich des RAM-Speichers. Gehen wir nun in die Unendlichkeit, muss die Auflösung unendlich fein - der Return-Stack unendlich groß sein, der Computer also unendlich viele RAM-Bausteine allein hierfür haben. Darüber hinaus würde der Computer auch unendlich lange rechnen müssen – und so viel Zeit kann nun endgültig niemand von uns aufbringen.
Dem allen zum Trotz hat das Thema eine praktische Anwendung ...
| Mithilfe der Hilbert-Kurve endlicher Iteration kann man die Teilquadrate und mithilfe des Limes die Punkte im Quadrat in eine lineare Reihenfolge bringen, die Hilbert-Ordnung genannt wird. Mit ihr lassen sich (effiziente) Verfahren, die auf einer linearen Ordnung beruhen, ins Mehrdimensionale übertragen. Dazu gehört binäres Suchen, binärer Suchbaum, Skip-Liste und andere. |
Und das sind noch ein paar der Die Zuordnung hn der Hilbert-Kurve einer (endlichen) n-ten Iteration ist umkehrbar und kann zu beliebiger Feinheit gesteigert werden. Dieses und die gute Nachbarschaftserhaltung hat eine Vielfalt von Anwendungen der Hilbert-Kurve in der Informatik eröffnet, so in der Bildverarbeitung, Datendarstellung, im Hochleistungsrechnen und in anderen Gebieten. |
Joachim hat jedenfalls mit der Hilbert-Kurve ein interessantes Thema aufgegriffen.
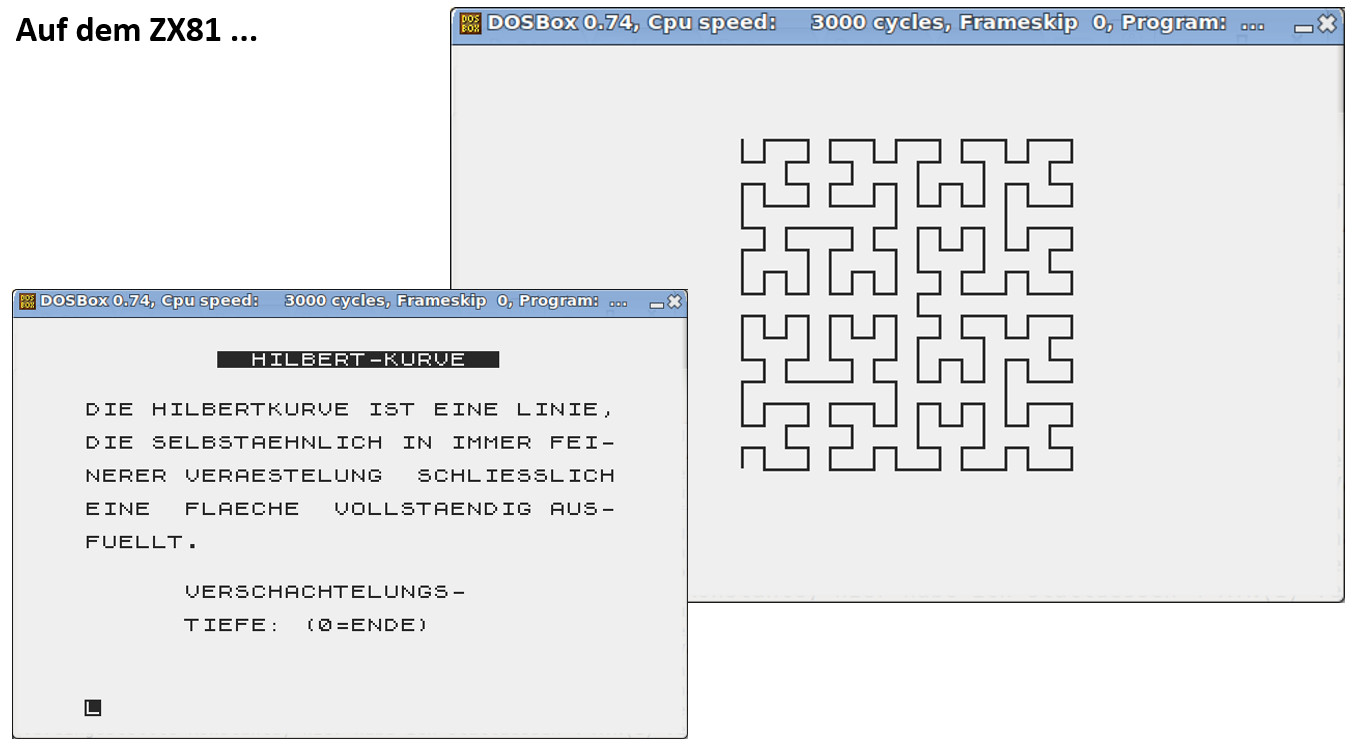
Heinz, eigentlich ein Spectrum-Mann, dachte sich, die Muster sollte man erst einmal auf dem Computermonitor begutachten und schrieb zunächst ein LOGO-Programm dafür (Läuft es auf unserer JOYCE? Freiwillige vor!) und anschließend eins für das Basic des ZX81.
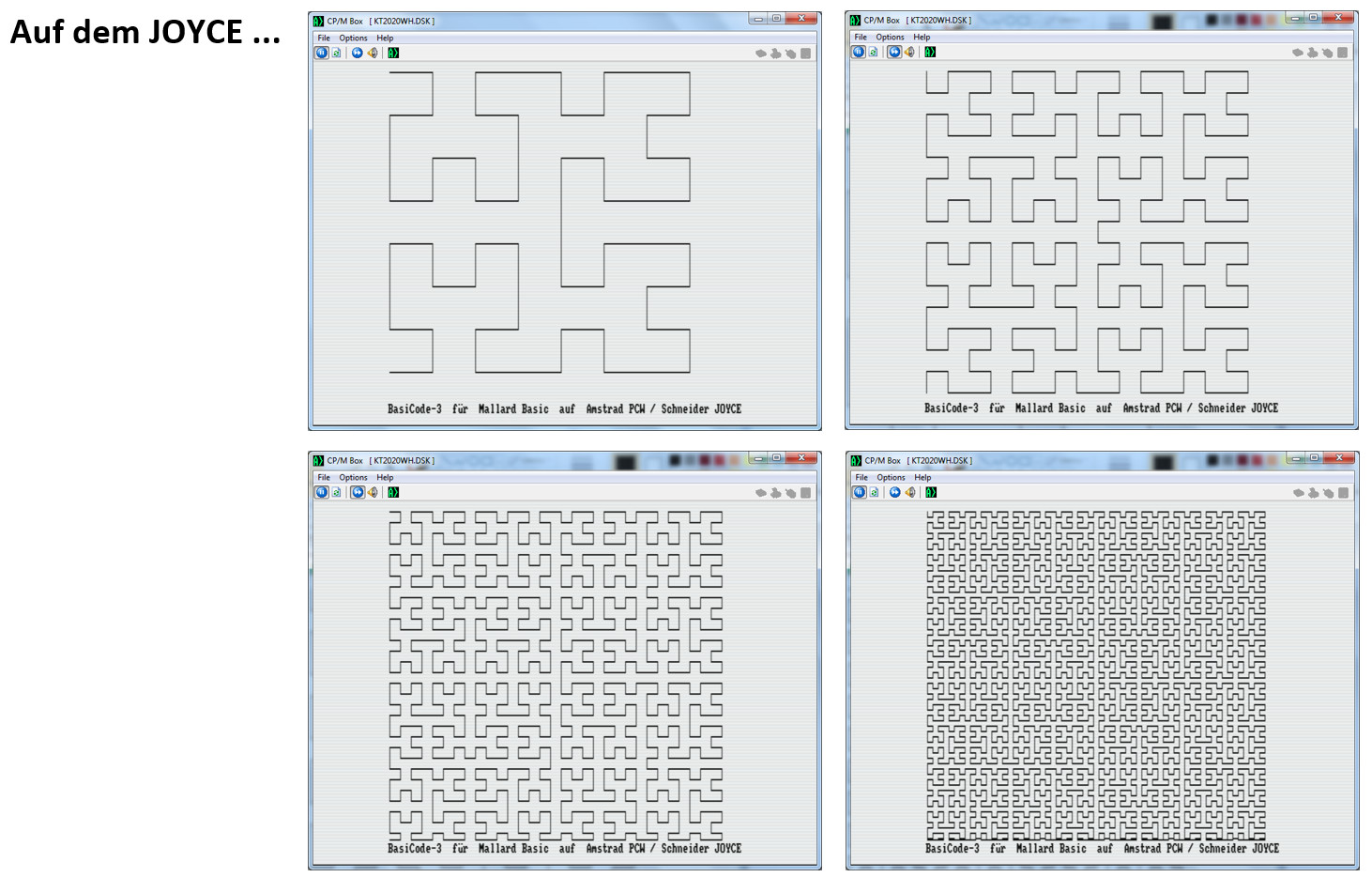
Mir kam (wen wundert es?) der Gedanke, Heinz' Programm in das BasiCode-System zu übertragen. Auf den ersten Blick klingt es umständlich, das Drumherum "aufzublasen". Doch es bringt den Vorteil, dass die übertragbare Hälfte des BasiCode-Programms dann auch sofort auf allen Computern genutzt werden kann, für die es BasiCode-3 gibt. Die Grafik-Befehle müssen nicht abgeändert werden, denn sie sind in der nicht-übertragbaren Hälfte verankert - der LINETO-Befehl wird einheitlich mit GOSUB 630 aufgerufen.
Unter BasiCode-Anwendern sind Programme mit selbstähnlichen Strukturen schon bekannt, zum Beispiel SCHNEEFL.ASC und SIERPINS.ASC, die unter dem Reiter "Programs" des online-Bascoders zu finden sind, wo sie auch gleich ausprobiert werden können. Um das Hilbert-Programm zu testen genügt es, es unter dem Reiter "Listing" hineinzukopieren, zum Starten einfach in das große linke Fenster klicken.
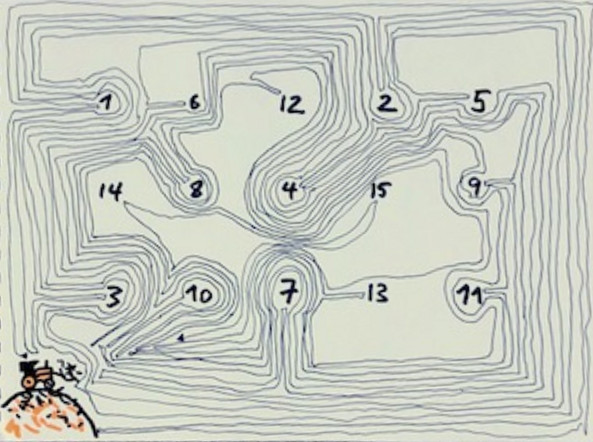
Es hat eine gewisse Faszination zuzuschauen, wie der Computer die Verästelungen zeichnet, ohne sich zu verhaspeln. Ich fühlte mich an ein Spiel aus der Grundschulzeit erinnert:
Im Schulhort spielten wir außer "Name, Stadt, Land" (in den alten Bundesländern bekannt als "Stadt, Land, Fluss") auch sehr gern "Mistfahren": Auf einem Blatt Papier werden kreuz und quer Zahlen z.B. von 1 bis 30 aufgeschrieben. Der erste Spieler kreist nun die 1 ein und zeichnet einen Weg zur nächsten Nummer (der 2) und kreist sie ein. Der zweite Spieler zeichnet von dort mit einer anderen Farbe einen Weg zur nächsten Nummer und kreist sie ein. Nun ist der erste Spieler wieder an der Reihe. Die anderen Nummern und immer mehr werdenden Linien dürfen weder berührt noch gekreuzt werden, sonst ist das Spiel für den ungeschickten Zeichner verloren.
Ob es die Kurzen heute noch spielen? Vermutlich nur, wenn es das auch als App für das Tablet gibt !?!
Ich habe mich so weit es ging an Joachims und Heinz' Vorlage gehalten und nur dort eingegriffen, wo ZX81 und die restliche Computerwelt nicht kompatibel sind. Zum Beispiel bemängeln manche BASICs, wenn es für eine GOSUB-Anweisung zwei RETURN-Anweisungen gibt, z.B. im THEN- und ELSE-Zweig einer IF-Anweisung. Die Verwendung von SIN und COS habe ich zwecks Zeitersparnis durch eine Variante der MOD-Funktion ersetzt.
|
Es gibt übrigens weitere solcher raumfüllenden Kurven, zum Beispiel hat Bernd ein Turbo-Pascal-Programm für Peano-Kurven geschrieben ... einfach 'mal einen Abstecher ins joyceforum.de wagen !
Thomas Rademacher // April 2021